Modelling Numbers
There is an interesting way of teaching numbers to children in our schools. If we really think about it, numbers are just characters. They have no values by themselves, but instead are attached value. It’s similar to a $100 bill and a $1 bill. We know that the $100 bill is worth more because it is a larger value, but we also understand that $100 can buy more things than $1.
A young learner just being introduced to numbers has to develop their understanding of numbers just as we may have forgotten that we did in the past. They have to learn the values of numbers, and usually this is done by representations of numbers using models. One common example is math problems involving cookies. You give a child two sets of cookies: one set has 4 cookies, the other set has 1 cookie. You don’t directly ask which set has more cookies but instead you attach some relatable knowledge they have by asking questions such as “Which set of cookies do you want to take?”
It seems like a silly question to ask, but for a child, the concept of “more” and “less” does not have a strong foundation, but eating 4 cookies is usually better than eating 1 cookie.
So how does this all relate to older learners?
Well, once we get past the initial “learning which numbers are bigger” within 1-10, we find ourselves with a more difficult problem: how do we give a child 1,000 or 10,000 or 100,000 cookies? It’s just not realistic to do. That’s where modelling numbers come in.
Some children find it difficult to decide which number has more when given larger numbers such as “7654” and “7564”. Number modelling breaks down larger numbers into smaller parts that can be represented with 1-10 but have an attached value to them such as ones, tens, hundreds, thousands, and so on. These number models allow us to give children physical representations of larger numbers without having to count out 100 pieces or more each time. Just seeing two abstract values is much more difficult than necessary so number modelling is one way to help your child understand larger number values.
A number model problem, in the third grade, looks something like this: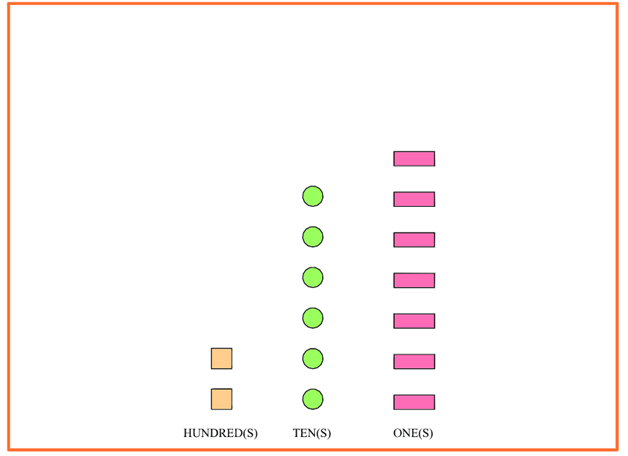
A number model problem is different across each textbook, school, and teacher. They may use different shapes in the problem, they may use real objects like apples, they may use animals, or they may use different colors. In the case of LI2EI, we opted for different shapes and colors. Each shape represents a specific number. In this case, the yellow squares are “Hundreds”. The green circles are “Tens”. The pink rectangles are “Ones”.
If your child counts each section out they will quickly see that there are:
Two hundreds (200)
Six tens (60)
Seven ones (7)
Putting these numbers together, the representation of the number shown in the number model diagram is 267.
Let’s take a look below at a few different ways your child could solve these number model problems.
Solution 1: Put the numbers together in a line
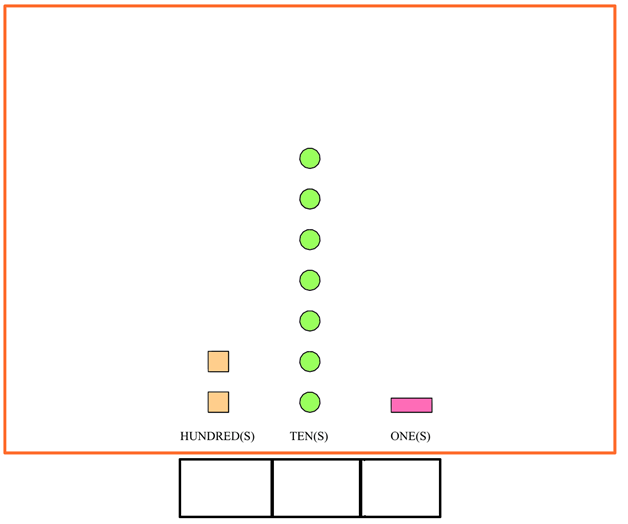
You can have your child set up the problems like how you see below: They draw a box under each number place and count the values in each column, giving you something like this:
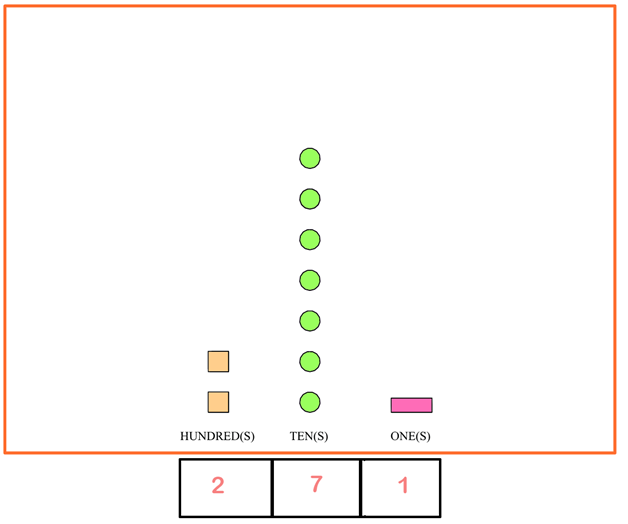
With the numbers falling into place on their own, your child can then see the number this diagram represents is 271 by just putting all the numbers together.
Solution 2: Expanded form numbers
Looking at the same problem, another way your child can solve the problem is by using the expanded form of numbers. They can set up the problem almost the same way but adding a few extras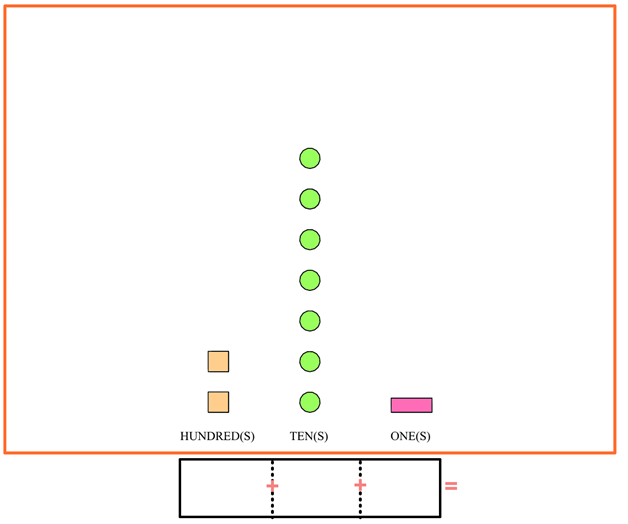
In this version, they are adding together the true value of each represented column. If they fill out the blanks, they’d end up with something like this:
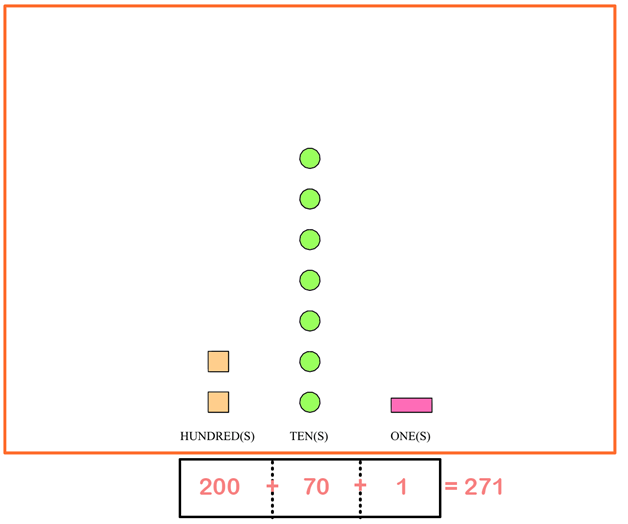
You may be wondering why we should complicate the number model problem. After all, the first solution type is extremely easy and can be solved in seconds. This second solution type is a way for your child to understand 0 values on numbers, adding numbers together with 0 values, and also to help them practice expanded forms of numbers (which was covered in another blog post). Both solutions help reinforce important concepts in math, so it’s good to practice both!
